摘 要：“彈性力學(xué)”課程是工科專業(yè)一門重要的專業(yè)基礎(chǔ)課，課程較為抽象，公式推導(dǎo)較多，學(xué)生普遍感覺難學(xué)。結(jié)合多年課程教學(xué)的經(jīng)驗，探討了“彈性力學(xué)”課程中力矩、內(nèi)力和方向余弦等量的正負號規(guī)定，明確說明了極坐標下各坐標軸的正負號規(guī)定，這是對教材的有效補充;將相容方程分為應(yīng)變、應(yīng)力和應(yīng)力函數(shù)表達式三類并進行了歸納，更便于學(xué)生理解;編制了彈性力學(xué)平面問題的可視化求解軟件，實現(xiàn)對圓筒受均布力、壓力隧洞、小孔口問題等十個典型問題的可視化求解，教學(xué)效果良好。

　　關(guān)鍵詞：彈性力學(xué);可視化;正負符號;相容方程

　　一、前言

　　“彈性力學(xué)”課程是工科專業(yè)一門重要的專業(yè)基礎(chǔ)課，是學(xué)習塑性力學(xué)、土力學(xué)的基礎(chǔ)，也是工科學(xué)生擺脫材料力學(xué)桿式構(gòu)件分析結(jié)果的束縛，向板、面和空間體分析拓寬的重要課程。該課程主要是通過考慮靜力學(xué)、幾何學(xué)和物理學(xué)三方面條件，在邊界上嚴格考慮受力條件和約束條件，建立微分方程和邊界條件來解決力學(xué)問題。課程對高等數(shù)學(xué)中的微積分、偏微分方程求解和級數(shù)，以及解析幾何、線性代數(shù)等知識的依賴性較高，且較為抽象，公式推導(dǎo)較多，學(xué)生學(xué)習普遍感覺較難。因此，開展“彈性力學(xué)”課程教學(xué)方法的研討十分重要。祝方才總結(jié)了彈性力學(xué)教學(xué)中的疑點[1]，論述了符號規(guī)定、差分公式和極坐標的推導(dǎo)三個方面的認識，提出了比教材更為清晰的推導(dǎo)過程。潘東輝采用 MATLAB 軟件提供的 PDE 工具箱對彈性力學(xué)中小孔口問題、圓環(huán)受內(nèi)外壓力作用等多個命題進行了計算分析[2]，指出該工具箱的橢圓型偏微分方程的解實質(zhì)是求解彈性力學(xué)平面問題的數(shù)值解法，可以方便求解彈性力學(xué)的平面問題，并且可以實現(xiàn)結(jié)果的可視化，是進行彈性力學(xué)教學(xué)的有力輔助手段。張偉偉提出了在教學(xué)實施中遵循先工程[3]，后數(shù)理，再力學(xué)的講解順序的三段式教學(xué)方法，便于學(xué)生理解和掌握。這些論述對提升彈性力學(xué)課程的教學(xué)效果有較大的促進作用。本文針對徐芝倫編著的彈性力學(xué)經(jīng)典教程——《彈性力學(xué)簡明教程》，結(jié)合多年工科專業(yè)“彈性力學(xué)”課程的教學(xué)實際，對課程教學(xué)中學(xué)生難掌握的幾個難點問題進行論述和推導(dǎo)，力求加深教師和學(xué)生對這些問題的理解。

　　二、符號規(guī)定

　　彈性力學(xué)求解中均是在一定的坐標體系下進行，對各個變量的符號有較為嚴格的規(guī)定，求解應(yīng)該在這個符號體系下進行，否則將得到不正確的結(jié)果。教材中對于應(yīng)力、應(yīng)變和位移，以及面力和體力符號均有明確的規(guī)定，但是對于力、力矩、剪力和極坐標下的部分符號的規(guī)定不明確，不利于學(xué)生的理解和掌握，需要進一步厘清。

　　(一)力矩 M 的符號規(guī)定

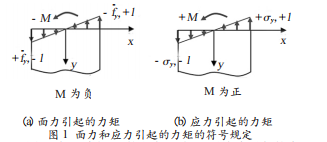
　　教材中講授平面問題時對于力矩的正負號規(guī)定沒有明確指出，而只是在講述薄板彎曲時才明確提到，但是在平面問題中，特別是列出圣維南原理的積分方程中需要明確力矩的正負號。力矩的正負號應(yīng)該分為應(yīng)力引起的力矩和外力引起的力矩兩類，兩者之間是有區(qū)別的。對于面力引起的力矩，也應(yīng)該先將力矩根據(jù)其作用方向概化為分布的面力(一般直接概化為直線分布最為簡單)，然后依據(jù)“面力符號與力臂符號相同時力矩為正;反之為負”的原則進行正負號的判斷，見圖 1(a)。對于應(yīng)力引起的力矩的正負規(guī)定應(yīng)該是：“應(yīng)力符號與力臂符號相同時力矩為正;反之為負”。確定應(yīng)力引起的力矩正負時，先應(yīng)該將應(yīng)力概化為沿正負兩側(cè)力臂的分布應(yīng)力(一般直接概化為直線分布最為簡單)，利用以上原則確定力矩的正負號，見圖 1(b)。

　　圖 1 看出，力矩 M的方向一致，但是應(yīng)力引起的力矩的符號為負，而面力引起的力矩為正，兩者符號不同，這是在負面上的情況。在正面上兩者的符號相同，主要原因是應(yīng)力和面力符號規(guī)定不同造成的，在列出圣維南原理的積分方程是應(yīng)該注意區(qū)分應(yīng)力和面力引起的力矩的符號區(qū)別。

　　(二)面力和體力的合力及內(nèi)力的符號規(guī)定

　　應(yīng)力是單位面積上分布的內(nèi)力，內(nèi)力是一種力，等于應(yīng)力乘以面積。在進行平衡方程推導(dǎo)時，要建立某一個方向上的平衡，也就是通過該方向上合力為 0 這一條件建立平衡方程時，需要確定內(nèi)力的正負號。內(nèi)力是一種力，是合力，其符號規(guī)定應(yīng)該是“與坐標軸指向相同的為正，反之為負”。內(nèi)力的方向與應(yīng)力的方向一致，但是其符號規(guī)定與應(yīng)力“正面正方向和負面負方向為正，反之為負”的規(guī)定不同，在正面上兩者相同，而負面上兩者相反。其他面力合力和體力合力的正負號規(guī)定也是“與坐標軸指向相同的為正，反之為負”。理解這些概念對平衡方程的推導(dǎo)有較大的幫助。

　　(三)方向余弦的符號規(guī)定

　　方向余弦是求解斜截面應(yīng)力所必需的參數(shù)，其意義在于邊界面的外法線方向的正方向與坐標軸正方向之間夾角的余弦值。在教學(xué)中發(fā)現(xiàn)，很多學(xué)生對其正負號如何確定不理解，影響對計算推導(dǎo)掌握。實際上，方向余弦的正負是按照余弦函數(shù)計算得到的，要理解其正負規(guī)定，應(yīng)該從夾角的意義理解，特別應(yīng)該知道兩個“正方向”之間的夾角的余弦這句定義。另外根據(jù)余弦函數(shù)的值的特性可知，不同象限的方向余弦正負不同，第一象限中不論 x 和 y 方向的方向余弦 l 和 m 均為正值;第二象限 x 方向的方向余弦為負值，y 方向為正值;第三象限 x 方向的方向余弦為負值，y 方向為負值;第四象限 x 方向的方向余弦為正值，y 方向為負值。實際判斷時應(yīng)該按照外法線方向所在的象限來判斷方向余弦的正負號。

　　(四)極坐標情況下的符號規(guī)定

　　極坐標與直角坐標是彈性力學(xué)求解的兩種坐標體系，但是在教學(xué)中發(fā)現(xiàn)學(xué)生對兩種坐標體系之間的聯(lián)系理解不深，應(yīng)該在講授中加以說明。實質(zhì)上，極坐標與直角坐標之間是緊密相關(guān)的，極坐標的方向離不開直角坐標;兩者之間的量是可以相互轉(zhuǎn)化的，也有密切的關(guān)系。極坐標中徑向 ρ 的正向就是從原點向外射線的方向，而環(huán)向 φ 的正向決定于相應(yīng)的直角坐標的 x 和 y 軸的方向，即以 x 軸轉(zhuǎn)向 y 軸的方向為正，不能按照逆時針或者順時針為正來確定，同時 φ的大小是徑向射線正向與 x 軸之間的夾角。

　　三、相容方程的歸納

　　相容方程是應(yīng)力法求解彈性力學(xué)問題的重要方程，引入應(yīng)力函數(shù)后問題的求解轉(zhuǎn)化為求解相容方程的問題。但是相容方程從幾何方程推導(dǎo)出后稱為變形協(xié)調(diào)方程，帶入物理方程等后還有用應(yīng)力表達的相容方程，各類相容方程之間的關(guān)系會造成學(xué)生理解的偏差，對其進行歸納總結(jié)便于學(xué)生對其深入理解掌握。對于直角坐標情況，相容方程可以分為應(yīng)變表達式、應(yīng)力表達式和應(yīng)力函數(shù)表達式三類，應(yīng)變表達式是從幾何方程中消除位移量后得到的方程，是相容方程的本質(zhì)方程，也稱為變形協(xié)調(diào)方程;應(yīng)力表達式是物理方程帶入相容方程的應(yīng)變表達式后得到的方程，表示各個應(yīng)力分量應(yīng)該遵循的關(guān)系方程;而應(yīng)力函數(shù)表達式是引入應(yīng)力函數(shù)后的表達式，是將求解應(yīng)力分量問題“消元” 后成為 1 個未知量 φ 后的相容方程。三者的關(guān)系與異同可歸納為表 1。

　　另外極坐標的相容方程教材中給出的表達式為：式中：Φ 為應(yīng)力函數(shù);ρ，φ為極坐標兩個軸。這一個表達式?jīng)]有展開，在學(xué)生進行某一個函數(shù)是否滿足相容方程的校核中有一定困難，應(yīng)該將其展開式列出。本文對該式進行了展開如下式(2)和(3)，這樣便于學(xué)生理解。

　　四、應(yīng)力分量的合成與應(yīng)力泡

　　王潤富編著的《彈性力學(xué)簡明教程學(xué)習》中第四章例題 6 關(guān)于劈裂問題的求解是一個很好的例子，對于學(xué)生理解半無限平面受集中力作用下應(yīng)力的分布問題的啟發(fā)性較好，且是講解彈性力學(xué)解答應(yīng)用的好例證。但是講解時應(yīng)該注意強調(diào)兩點，其一為應(yīng)力的合成方法，其二是應(yīng)力泡的概念。

　　1.應(yīng)力分量的合成方法。應(yīng)力是一個張量，一點的應(yīng)力要通過過該點的平行六面體上的所有應(yīng)力分量來描述，這些量值中只有(σx，σv，σz，τxv，τvz，τx)六個量是獨 z 立的。同時一點的應(yīng)力也可以用三個主應(yīng)力和其方向決定。應(yīng)力的合成原則是“作用于同一個面上的應(yīng)力分量可以合成為一個應(yīng)力全量，不同面上的應(yīng)力分量不能合成”。只有建立這個概念才能理解應(yīng)力的特性，也才能做對例題 6。

　　2.應(yīng)力泡的概念。集中力 F 作用下半無限平面內(nèi)過集中力作用點的直徑為 d 的圓，這個圓上的應(yīng)力值為：也就是說在這個圓上任意一點，其受力類似單軸受壓，壓應(yīng)力就等于 σp 值，圓周上任意點的應(yīng)力均相等，且應(yīng)力值的大小隨直徑 d 的增大而減小，這就是通常所說的應(yīng)力泡。講解時應(yīng)強調(diào)其應(yīng)力主面就是徑向和環(huán)向兩個面，其應(yīng)力的方向各點是不同的，應(yīng)力的大小隨著應(yīng)力泡直徑的增大而增大，也就是隨深度的增大而衰減。同時應(yīng)將與大面積堆載時，應(yīng)力不隨深度增大而減小的實際進行對比，強調(diào)兩者的區(qū)別。

　　五、彈性力學(xué)平面問題可視化軟件

　　在“彈性力學(xué)”課程的教學(xué)中，經(jīng)常有復(fù)雜的數(shù)學(xué)公式和抽象的計算，不利于學(xué)生的理解。倘若在教學(xué)中，能夠通過一些教學(xué)小程序使計算出來的抽象的數(shù)值變成一些可視化的圖形，教學(xué)將變得更加生動，同時也利于學(xué)生接受。因此利用 Visual Basic 編程語言的繪圖能力，編制了一些簡單平面問題的可視化求解軟件。主要目的是使一些簡單問題的解題結(jié)果可視化，輔助教師的教學(xué)，使學(xué)生能對抽象的計算結(jié)果有更加清晰直觀的理解，引導(dǎo)學(xué)生進行深入思考。軟件中選擇了懸臂梁受集中荷載、梁受均布荷載、圓筒受均布力、壓力隧洞、小孔口問題、平面應(yīng)力與平面應(yīng)變問題、邊界條件、擋水墻、楔形體、半平面體邊界上受集中力總十個典型的問題進行求解。其基本界面展示如下圖 2。每一個典型問題軟件均實現(xiàn)了正確求解，并可以改變輸入?yún)��?shù)得到不同的解答。軟件將抽象的計算結(jié)果轉(zhuǎn)變?yōu)榭梢暬�的圖形呈現(xiàn)給學(xué)生，便于學(xué)生理解和掌握。可視化求解軟件還在教材的基礎(chǔ)上補充了教材未涉及的內(nèi)容。例如：教材上壓力隧洞問題中僅展示了 n<1 時應(yīng)力分布的圖像，而求解軟件通過改變參數(shù)能將 n>1 和 n=1 時的計算結(jié)果和圖形展示出來，將課本上的抽象計算結(jié)果可視化地展示出來，并在教材解答的基礎(chǔ)上進行擴展延伸，從而引發(fā)學(xué)生的深入思考，激發(fā)學(xué)生的學(xué)習興趣。軟件界面分為三部分。第一部分載入這道題目的相關(guān)信息，包含題干、問題的示意圖和使用半逆解法求解出的應(yīng)力分量表達式。第二部分為數(shù)據(jù)輸入部分，在這個部分，使用者可以根據(jù)需要輸入問題的基本參數(shù)，為下一步計算應(yīng)力分量做準備。第三部分為結(jié)果輸出部分，用于顯示計算和繪圖的結(jié)果。在實際教學(xué)中該軟件對學(xué)生理解彈性力學(xué)解的實質(zhì)內(nèi)涵，理解應(yīng)力函數(shù)的分布空間規(guī)律幫助較大，教學(xué)效果良好。

　　六、結(jié)論

　　1.“彈性力學(xué)”課程中諸多符號的正負號規(guī)定較為嚴格，也極易弄錯，教材中對其的規(guī)定稍顯模糊。本文對力矩、面力和體力的合力、內(nèi)力和方向余弦的符號規(guī)定做了較為仔細的規(guī)定，并對極坐標下各個坐標軸的正負號規(guī)定進行了明確的說明，可用于教學(xué)實踐。

　　2.相容方程是“彈性力學(xué)”課程較為重要的概念，它有三種表達形式。本文總結(jié)歸納為應(yīng)變表達式、應(yīng)力表達式和應(yīng)力函數(shù)表達式三類，對其由來和意義進行了歸納說明，更便于理解和把握。

　　3.為了提高教學(xué)效果，編制了彈性力學(xué)平面問題的可視化求解軟件，軟件可以實現(xiàn)對十個較為典型問題的彈性力學(xué)問題的求解，如：懸臂梁受集中荷載、梁受均布荷載、圓筒受均布力、壓力隧洞、小孔口問題、平面應(yīng)力與平面應(yīng)變問題、邊界條件、擋水墻、楔形體、半平面體邊界上受集中力。軟件實現(xiàn)了對計算結(jié)果的圖形化顯示，便于學(xué)生理解抽象的函數(shù)，教學(xué)效果良好。

　　參考文獻：

　　[1]祝方才，肖宏彬，歐陽建湘.彈性力學(xué)教學(xué)中的幾個疑點問題[J]. 株洲工學(xué)院學(xué)報，2004，(2).

　　[2]潘東輝，馬崇武.MATLAB/PDE 在彈性力學(xué)可視化教學(xué)中的應(yīng)用[J].力學(xué)與實踐，2014，(4).

　　[3]張偉偉，田錦邦.彈性力學(xué)的三段式教學(xué)方法[J].力學(xué)與實踐，2017，(2).

　　“彈性力學(xué)”教學(xué)中幾個難點問題的探討相關(guān)論文期刊你還可以了解：《《應(yīng)用力學(xué)學(xué)報》科技期刊論文發(fā)表》