摘要：目前基于彈塑性有限元的強度折減法已被廣泛應用于巖土工程邊坡穩定性分析當中，但是，這一方法在折減原理（即如何折減）、失穩判據和安全系數的選取以及屈服準則的選用上都存在較大的爭議。筆者基于此，根據目前的研究現狀，針對上述幾方面作了綜合性的探討，期望能對該理論研究提供參考。
　　關鍵詞：邊坡，穩定性，強度折減法
　　
　　1.前言
　　目前，對于邊坡穩定的設計計算大都采用強度儲備的方法，即令邊坡穩定性安全系數，這里為達到極限平衡狀態時的強度折減系數。通過這一折減措施，從而可以保證工程具有一定的安全度。如今，隨著有限元這一計算工具的出現，其與強度折減的結合，使之具有了其他傳統條分法所無法比擬的優越性，因而被廣泛應用于邊坡穩定的計算當中。但是，這一方法在如下幾方面還存在較為廣泛的爭議：
　　2.正文
　　2.1.折減原理
　　Duncan(1996)指出，邊坡安全系數可以定義為使邊坡剛好達到臨界破壞狀態時，對土的剪切強度進行折減的程度。
　　通過逐步減小抗剪強度指標，將、值同時除以折減系數，得到一組新的強度指標、，進行有限元計算分析時，反復計算直至邊坡達到臨界破壞狀態，此時采用的強度指標與巖土體原有的強度指標之比即為該邊坡安全系數，計算公式如下：
　　、（1）
　　趙尚毅、鄭穎人等[1]通過比較畢肖普法（其安全系數定義為：沿整個滑動面的抗剪強度與實際抗剪強度之比，即：）和強度折減法的安全系數定義，認為兩者安全系數具有相同的物理意義，強度折減法在本質上與傳統方法是一致的。
　　鄭宏等[2]人則認為：通常情況下，巖土材料的抗剪強度和越大，其彈性模量也越大，泊松比就越小。所以在通常利用強度折減法進行邊坡穩定性計算時，也應對和作相應的調整。
　　葛修瑞院士[3]也提出“僅將、值同時除以相同的折減系數是否合理？”這一疑問。事實上，在不同類型的邊坡工程中，在維持邊坡穩定性方面，、值所作的貢獻是有差別的，并且、可以變動的范圍也大不相同，而且從物理意義上來講兩者屬不同的力學屬性。但是如果使用不同的折減系數，即和，那么問題就復雜化了，可以得到無窮多的和的組合解，這也就不再能成為安全系數的定義。
　　另外，當潛在滑動面切過性質不同的介質時，這些介質的、值很不相同，此時還是用統一的強度折減系數作為邊坡的安全系數更是顯得非常勉強。
　　2.2.失穩判據及安全系數
　　如何在不斷降低巖土體強度參數的過程中判斷是否達到臨界破壞狀態，這是有限元、有限差分計算中經常遇到的比較棘手的問題。目前強度折減法的破壞標準主要有以下幾種：（1）以有限元數值計算不收斂作為邊坡失穩的標志；（2）以廣義塑性應變或者等效塑性應變從坡腳到坡頂貫通作為邊坡破壞的標志；（3）以特征部位位移突變為標志。
　　鄭穎人等[4]主張在強度折減有限元方法分析邊坡的穩定性時，采用了有限元解的不收斂作為破壞標準，但是解不收斂后的應力應變往往是無法確定的，再加上可能導致有限元解的不收斂的因素很多，因此，以解的不收斂性作為其判據并不一定具有通用性；
　　宋二祥等[5]采用某個部位位移作為評判標準；特征部位的位移突變應該說是模型破壞的必要條件，但并不是充要條件。在某些大型滑坡的計算中，往往還會伴隨多個次級滑坡，這時觀測點的選擇就顯得尤為重要；
　　連鎮營等[6]認為邊坡破壞的特征是某一幅值的廣義剪應變從坡腳到坡頂上下貫通，則此前的折減系數即為邊坡的安全系數；但是有眾多的學者對此提出質疑：邊坡塑性區從坡角到坡頂貫通并不一定意味著邊坡整體破壞，塑性區貫通也是破壞的必要條件，但不是充分條件，破壞與否還要看塑性應變是否具備繼續發展的邊界條件；
　　劉金龍，欒茂田等[7]主張聯合考慮特征部位位移突變性和塑性區的貫通性作為失穩判據。黃正榮、梁精華[8]則認為應以邊坡上測點位移增量與強度折減系數增量的關系曲線來確定安全系數，當水平位移增量與強度折減系數增量之比急劇變化時，則認為開挖面處于臨界破壞狀態，此時的強度折減系數即為邊坡穩定的安全系數。
　　總而言之，對于其失穩判據選取以及如何選取目前是眾說紛紜，相應確定的安全系數也各不相同。筆者傾向于用超載法求取邊坡穩定安全系數，即逐步增大荷載倍數至邊坡失穩（例如：取解不收斂為判據），此時荷載放大倍數即為超載安全系數。這種做法與前面方法相比具有兩方面的優勢：①經過強度折減后的計算模型及其應力狀態是一個虛擬的情形，而超載法顯然反映的是真實邊坡實際破壞的情形，從理論上講計算結果更合理一些；②從算法上看，邊坡上作用荷載是破壞荷載的（注：），這樣就可以將失穩判據引起的誤差降低倍，而前述方法則剛好相反。
　　2.3.強度屈服準則
　　邊坡穩定性分析其計算結果與所選的本構關系和強度屈服準則都有很大關系。當巖土體的本構關系采用理想彈塑性模型，屈服準則為廣義的米賽斯（Mises）準則：
　　即：
　　式中，，分別為應力張量的第一不變量和應力偏張量的第二不變量。這是一個通用表
　　表1.各參數的選取

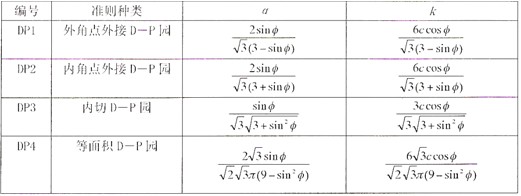
　　達式，通過變換、的表達式就可以在有限元中實現不同的屈服準則。、是與巖土材料內摩擦角和內聚力有關的常數。
　　傳統的極限平衡法采用摩爾－庫侖準則，但是由于摩爾－庫侖準則的屈服面為不規則的六角形截面的角錐體表面，存在尖頂和菱角，給數值計算帶來了困難，為了與傳統方法進行比較，徐干成、鄭穎人[9]（1990）提出的摩爾－庫侖等面積園屈服準則代替傳統摩爾－庫侖準則即DP4。此外，不同的、在π平面上代表不同的園[10]（如圖1所示）：
　　因此，單是使用D－P準則，就會存在外角點外接園、內角點外接園、內切園和等面積園，其計算結果就各不相同，直接采用M－C準則其計算結果顯然與D－P也不相同，這樣不同的人采用不同的屈服準則就會得到不同的安全系數和不同的滑移面位置，這就難免會對這種強度折減法的計算結果的合理性和可靠性產生懷疑。另一方面，在使用強度折減法計算時，若邊坡接近極限破壞狀態時，往往會導致計算趨向于不收斂。
　　3.結論與展望
　　強度折減法的思路清晰，原理簡單，其與計算機技術相結合的彈塑性有限元方法已被廣泛應用于巖土工程領域。但計算結果是否準確，一方面與計算方法是否精確、強度理論是否正確、失穩判據是否合理、所建模型是否準確等有關；另一方面利用有限元方法計算邊坡穩定性時，土性參數的選取所帶來的誤差往往遠大于計算方法和本構模型所引起的誤差。因此，土性參數選取的合理與否對于計算結果的影響也是至關重要的。
　　此外，目前大多文獻將強度折減法僅局限用于平面應變下的二維邊坡穩定性的研究中，對于三維邊坡穩定性的應用研究較少，而實際邊坡都是屬于三維空間狀態，因此對于三維情況下的適用性及失穩判據和安全系數的影響有待進一步的研究。
　　參考文獻
　　[1]趙尚毅,鄭穎人,時衛民等.用有限元強度折減法求邊坡穩定性安全系數.巖土工程學報,2002,24(3):344–346
　　[2]鄭宏，李春光，李焯芬等.求解安全系數的有限元法[J].巖土工程學報，2002，24(5)：323－328
　　[3]葛修潤.關于邊坡與壩基抗滑穩定問題的“矢量和”分析方法（第九屆全國巖土力學數值分析與解析方法研討會特邀報告）.武漢：中國科學院武漢巖土力學研究所，2007.10
　　[4]鄭穎人,趙尚毅,張魯渝.用有限元強度折減法進行邊坡穩定分析.中國工程科學,2002,4(10):57–61
　　[5]宋二祥.土工結構安全系數的有限元計算.巖土工程學報,1997,19(2):1-7
　　[6]連鎮營,韓國城,孔憲京.強度折減法研究開挖邊坡的穩定性.巖土工程學報,2001,23(4):407-411
　　[7]劉金龍，欒茂田等.關于強度折減有限元方法中邊坡失穩判據的討論.巖土力學，2005，26（8）：1345-1348[8]黃正榮，梁精華.有限元強度折減法在邊坡三維穩定分析中的應用.工業建筑，2006（6）：59-64
　　[9]徐干成,鄭穎人.巖土工程中屈服準則應用的研究.巖土工程學報,1990(2):93-99
　　[10]趙尚毅,時衛民,鄭穎人.邊坡穩定性分析的有限元法.地下空間,2001,21(5):450–454      論文網